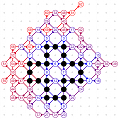
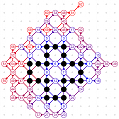
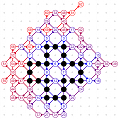
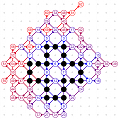
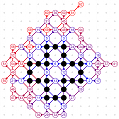
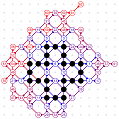
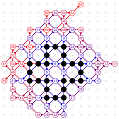
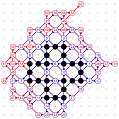
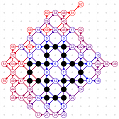
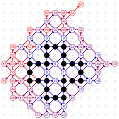
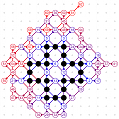
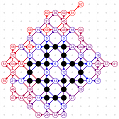
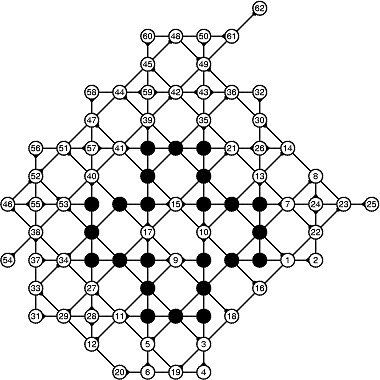
March-April 2008: the 12 different 4T record grids of 62 moves by Michael Quist. The differences being subtle, click on the images to compare them.
Morpion Solitaire - Record Grids (4T and 4D games)
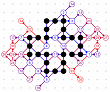
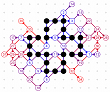
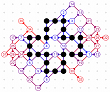
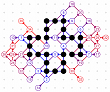
March-April 2008: The 4T and 4D games are solved! With the enumeration done by Michael Quist, we know that the 4T and 4D records of Heikki Hyyrö and Timo Poranen, who were the first to find grids of 62 and 35 moves, will NEVER be beaten! The 4T game cannot reach 63 moves, and there are 12 different record grids of 62 moves. Here are these record grids, they have exactly the same dots, only their lines are sligthly different. The Hyyrö-Poranen grid is the fourth one.












March-April
2008: the
12 different 4T record grids of 62 moves by
Michael Quist. The differences being subtle,
click on the images to compare them.
Similarly, the 4D game cannot reach 36 moves, and there are 4 different record grids of 35 moves. The Hyyrö-Poranen grid is the first one:
March-April
2008: the
4 different 4D record grids of 35 moves by
Michael Quist. The differences being subtle,
click on the images to compare them.

 Heikki Hyyrö (1976 - ) and Timo Poranen (Tampere 1974 - )
Heikki Hyyrö (1976 - ) and Timo Poranen (Tampere 1974 - )
The two records of 62 and 35 moves were set in October 2007 by Heikki Hyyrö and Timo Poranen, Department of Computer Sciences, University of Tampere, Finland. They gave these grids in their "New Heuristics for Morpion Solitaire" paper. Their homepages are http://www.cs.uta.fi/~helmu/index_e.html and http://www.cs.uta.fi/~tp
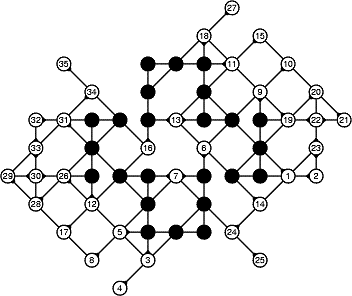
October
2007: Grids of 62 and 35 moves done by computer by Heikki
Hyyrö and Timo Poranen
It seems that the first study of the 4T and 4D games started much later than the 5T and 5D games: it was by Erik D. Demaine, Martin L. Demaine (both from MIT, USA), Arthur Langerman and Stefan Langerman (University of Brussels, Belgium) with these grids of 56 and 31 moves of their "Morpion Solitaire" paper first published in 2004, and again in the improved version of their paper in 2006.
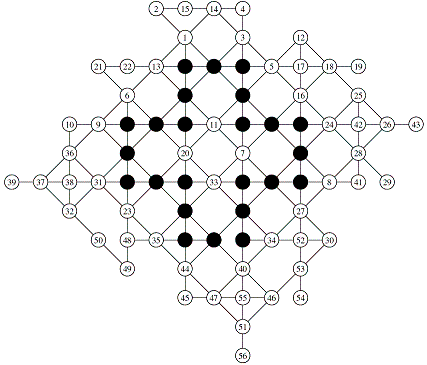
May
2004: Grids of 56 and 31 moves
by Erik D. Demaine, Martin L. Demaine, Arthur Langerman, and Stefan Langerman.
From
their "Morpion Solitaire" paper, Theory of Computing Systems, vol. 39
(2006), these grids are the figures 6 and 5, page 445.
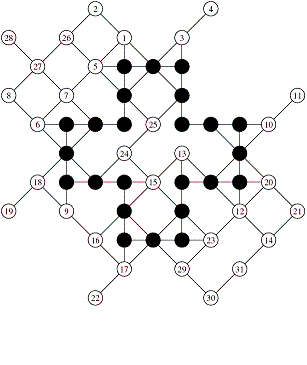
These grids of 60 and 34 moves done by hand have a very nice property: they are symmetical around the center. Better than the Demaine et al grids, and only respectively two less moves and one less move than the records.
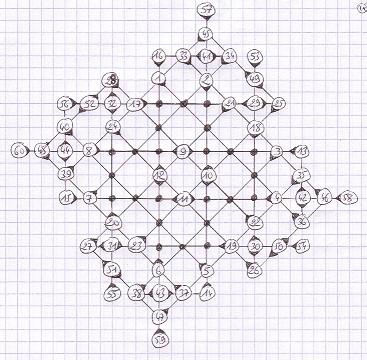
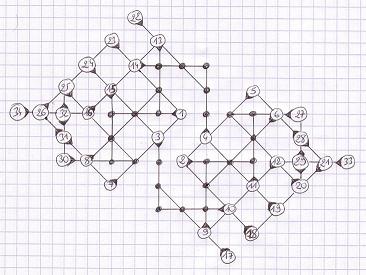
January 2008: Grids of 60
and 34 moves by Christian Boyer. Look at their symmetry around the center
After his enumeration, Michael Quist confirmed that this score of 34 moves is maximal for grids with inversion symmetry in the 4D game, and that there are exactly 33 distinct maximal grids with that symmetry. And Michael also confirmed that 60 moves is maximal for grids with inversion symmetry in the 4T game, and that there are 5 distinct maximal grids with that symmetry.
© Christian Boyer, www.morpionsolitaire.com