Morpion Solitaire - Variants

In this page:

Connector (two players)

Walter Joris by himself in 2002 (from his book page 7)

In his book "100 Strategic Games for Pen and Paper", Walter Joris published this game for two players called "Connector". Here it is as he published it, thanks to his kind authorization. This book is also translated and published in Spanish, Polish and Greek.

   
100 Strategic Games for Pen and Paper (Carlton Books, 2002). For the "Connector" rules, click to enlarge the image on the right.

We may think that there is an easy winning strategy for the second player: always play the central-symmetrical move of the first player. I received this remark in March 2008 from Vincent Everaert, the author of the Morpiae game detailed in the following part of this page. Michael Quist proposes an easy additional rule keeping the game interesting: "let the first player (only) place a single additional point within the cross before play begins, which breaks the symmetry."

But the first player can himself break the symmetry, and therefore the strategy of the second player. Here is a beginning of a game sent in January 2014 by Maria Eichlseder, Institute for Applied Information Processing and Communications (IAIK), Graz University of Technology, Austria, (http://www.iaik.tugraz.at/content/about_iaik/people/eichlseder_maria/). If the first player's move is a diagonal line crossing the center, then, obviously, the second player can no more play the central-symmetrical move. This should be the ONLY case: no horizontal or vertical line can block the second player, no diagonal line not crossing the center can block the second player.


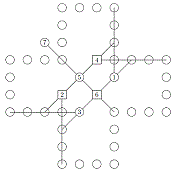
Counter-example of the winning strategy of the second player, by Maria Eichlseder, January 2014
The second player can't play his move 8 central-symmetrical to the move 7 of the first player. Click to enlarge the image.

Morpiae (two players)

Vincent Everaert, a French inventor of several games (see his website http://vincent.everaert.perso.sfr.fr), published in 2004 in Tangente Jeux & Stratégie another Morpion Solitaire variant for two players. He also wrote free Windows software to play this game:

The rules are briefly described in English in the above Zillions of Games webpage, and fully described in French in his paper below. The game is finished when no further move is possible, and the winner is the player having the maximum number of colored points.

     
Tangente Jeux & Stratégie n°11, Nov.-Dec. 2004. For the "Morpiae" rules, click to enlarge the image on the right.

Finite 3D/3T (one player)

Because 3D and 3T games from the standard initial pattern always seem infinite, it is interesting to search for other initial patterns allowing finite 3D and 3T games.

From this initial pattern using a cross smaller than the standard pattern, even if it is still easy to generate an infinite score, it is now possible -but very difficult- to get finite scores at the 3D game. The smallest possible score that I have found is a game with 23 moves. Is it possible to get a smaller score?

Using this same initial pattern, it seems impossible to get a finite score for the 3T game. Am I right, or will you find a finite grid?


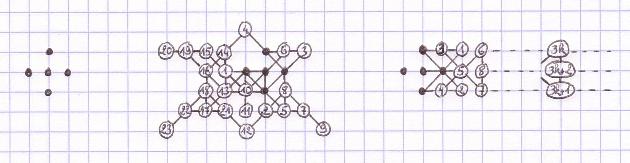
With this initial pattern at Finite 3D/3T, easy to get infinite grids, but difficult to get finite grids.
March 2008: 3D grid of 23 moves, by Christian Boyer.

In December 2011, Michael Quist computed the numbers of distinct possible grids for the first 20 moves of finite 3D, none of these grids is finite! This means that the smallest score N is : 21 ≤ N ≤ 23.

Number of distinct grids

Move No

Finite 3D

1

2

2

11

3

41

4

182

5

870

6

4268

7

20348

8

93287

9

412591

10

1777469

11

7500990

12

31065049

13

126069994

14

500075924

15

1935406164

16

7302276390

17

26876695302

18

96680779037

19

340549953872

20

1176446002170

≥ 21

Unknown ≠ 0

Scaffold (one player)

In his papers of April 1976 and February 1977, Pierre Berloquin mentioned a game close to Morpion Solitaire named "Scaffold", invented by C. Croft, and published in 1975 in the English magazine Games and Puzzles. I posed the question to Eric Solomon who has a complete index of this magazine at http://www.ericsolomon.co.uk/gpindex.html. He kindly sent me this short article (see below) as published in the Puzzle pages compiled by David Wells. Pierre Berloquin also mentioned a construction method of a scaffold of infinite height found by Harte and Brakes, but Eric Solomon did not find this answer in his Games and Puzzles collection. I also posed the question to David Wells; he does not remember hearing of Harte and Brakes or of any published answer to Croft's problem.

                           
On the left: C. Croft's problem published by David Wells in Games and Puzzles, issue 40, September 1975, page 36.
On the right: Harte and Brakes's solution of infinite construction published by Pierre Berloquin in Science & Vie, February 1977, page 122.
(the three black squares are the three direct first moves starting from the nine black circles of the initial pattern)

5T in a square (one player)

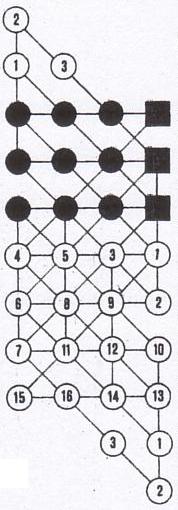
Richard Cotté, mathematics teacher, played a variant of the 5T game when he was a young student in 1970. The goal was to complete the square in which the starting cross is inscribed.

This variant is not obvious... here is a solution!


A solution to 5T in a square, by Richard Cotté
(click to enlarge the image)

Tsunami! (one player)

It is mathematically proved that a 5T game can't be infinite with a finite number of initial dots, as it is with the 36 dots of the initial cross.

But is it possible to fully fill the plane with an initial pattern, so infinite, but partially occupying the plane?

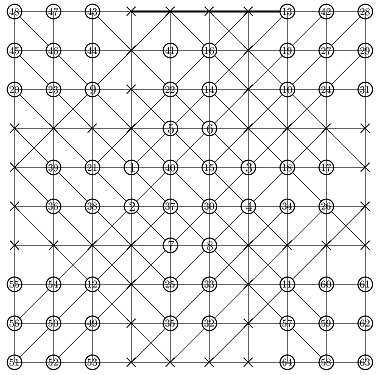
Here is a solution found by Michel Criton in 1976, and published by Pierre Berloquin in Science & Vie, February 1977. The initial pattern occupies a small band (and only one) of four dots wide, with repeated 4x3 rectangles. Using 5T rules, after a first "wave" of dots and lines, the band is one dot larger on each side. After a second "wave", the band is two dots larger on each side. After a third "wave", the band is three dots larger on each side. After a fourth "wave", the band is four dots larger on each side.

Then, with these new bands of four dots that we have generated on each side, we can infinitely reproduce similar series of four waves: a tsunami, infinitely filling the plane!

               
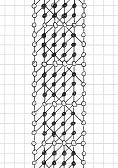
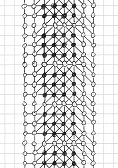
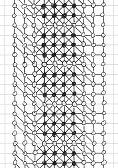
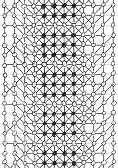
Initial pattern, and the first series of four waves of the tsunami, by Michel Criton

Is it possible to produce a tsunami with a less dense initial band / pattern?

© Christian Boyer, www.morpionsolitaire.com