Morpion Solitaire - Score Limits
It is impossible to have an infinite number of
moves at Morpion Solitaire. Any game has a number of moves within these
limits:
|
Game (1)
|
Minimum score
|
≤
|
Current
record score (2)
|
≤
|
Upper bound (3) for
maximum score
|
|
5
|
T
|
20
|
≤
|
178
|
≤
|
705
|
|
D
|
82
|
121
|
|
4
|
T
|
22
|
62
|
192 62
|
|
D
|
16
|
35
|
48 35
|
Notes:
(1) The 5T, 5D, 4T, 4D games
are respectively called G'4(A4), G4(A4),
G'3(A3), G3(A3) in the Demaine
et al. paper.
(2) Or also "Lower bound for maximum score", proved
by the record grid.
(3) For the 4T and 4D games, it is not an upper
bound but the true maximum score. Thanks to the enumeration of Michael
Quist, we know now that any 4T game has a maximum of 62 moves and that any
4D game has a maximum of 35 moves .
We can also note than, by definition of their
rules, a 5T record score CAN'T be better than 5T+/5T#/5T++ record scores (games
with more free rules), themselves
limited by the same upper bound:
|
5T record
|
≤
|
5T+/5T# records (1)
|
≤
|
5T++ record
|
≤
|
Upper bound
|
|
178
|
≤
|
216
|
≤
|
317
|
≤
|
705
|
|
190
|
Note:
(1) Based only on
their rules, we can't say anything about 5T+ versus 5T# record scores.
Mathematical proofs
Demaine-Demaine-Langerman-Langerman mathematically proved
5D (141), 4T (192) and 4D (48) upper bounds in their "Morpion Solitaire" paper.
For the 5T game, they proved an upper bound of
838 moves in their 2004 version, improved to 704 moves in their 2006 version. However, two
small errors in their 2006 paper:
- error page 5, instead of 704 moves, their upper
bound should be 705 moves, because of a mistake in a formula, omitting a
term (error found by Flammenkamp, in Nov. 2011)
- error page 8, instead of 324 moves, Flammenkamp’s
upper bound is 288 moves, because his number includes the 36 initial dots
(error found by me, in Oct. 2011)
|
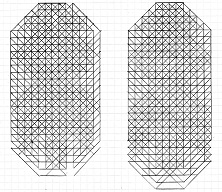
March
2003: Grids of 288 moves claimed to be upper bounds by Achim Flammenkamp
(image created in Oct. 2011 by
Christian Boyer, click to enlarge)
|
Before, in
March 2003, Achim Flammenkamp (University of Bielefeld, Germany) found exactly
the same upper bound of 705 moves and this tighter upper
bound of 288 moves only,
but Demaine et al. were "unable to verify
his proof sketch" (page 8 above). Here is this proof sketch:
The grids of 324 dots described
at the end of his proof are saided to be upper bounds. However,
even if they correctly contain 324 dots, they can't include
the needed 324 - 36 = 288 lines as you can check in my nearby image of
his two limit octagons: the first one with b1 = 14, b2 = 26, d1
= d2 = 31 can contain a maximum of 264 lines of five dots, and the second one with b1 = 13, b2 = 28, d1
= d2 = 32 can contain a maximum of 270 lines of five dots.
Below
my final 5T grid of 317 moves correctly contains the needed 317 lines and, because
this number is greater than his 288
moves, this proves that his result is not an upper bound:
his proof of 288 moves is wrong, why is it self-limited
to octagonal shapes? But the proof of 705 moves,
found both by him (= 741 - 36) and by Demaine et al. (= 704 +
1), seems correct.
November 2011, new
version of Flammenkamp proposing, page 10, a 5T
upper bound of 665 moves.
|
In the columns of Science & Vie, various
attempts to find 5T upper bounds were reported, but without detailed and/or valid proof:
- 540 by Daniel Goffinet and Pierre
Berloquin, June 1974 (Daniel Goffinet is the inventor of the "potential"
notion, reused by Berloquin, then by Demaine et al.)
- 556 by P. Bertin, June 1974
- 1021 by Robert Féron, M. Colmard,
and Pierre Berloquin, November 1974
- 144² = 20,736 by Daniel Goffinet
and Pierre Berloquin,
May 1975
- probably 500 or 600 estimated by Pierre
Berloquin, November 1975
There is another
5T upper bound obtained in the 70's:
In
August 2010, Pekka Karjalainen, Oulu, Finland, sent me a proof of a 5D
upper bound of 138 moves, three fewer moves than the Demaine et al. upper bound.


 Conference by Yushi Uno on his new upper bound, at CCCG 2013
Conference by Yushi Uno on his new upper bound, at CCCG 2013
In July 2013, Akitoshi Kawamura (University
of Tokyo, Japan), Takuma Okamoto, Yuichi Tatsu, Yushi Uno,
and Masahide Yamato (all four from Osaka Prefecture University,
Japan) proved a new 5D upperbound of 121 moves. This proof, version 1 published
in arXiv, was announced at CCCG
2013, the 25th Canadian Conference on Computational Geometry held
in August 2013 in Waterloo, Ontario, Canada.
In January 2014, they published
in arXiv a version 2 of their paper, retaining the upperbound of 121 moves,
but correcting a small flaw (part 4.2, new lemma 2 replacing old lemmas 2 &
3), and specifying that Peter Bartsch was the
first author of a grid of 102 moves (figure 3,
partie 4.3).
5T++
Record Grid (best
known 5T final grid): 317 moves
Because at each move of the game we simultaneously add one
dot and one line, any 5T (and also
5T+ and 5T#) grid
of n moves always has, during the game or at the end of the game:
- n + 36 dots, because the initial cross has
36 dots
- n lines of five dots (or lines of four segments if you
prefer)
What is the largest possible number of moves in
a final grid respecting these rules? "Final grid" means that we
do not check if it is possible or impossible to really
play this grid move by move from the initial cross.
Here is my best result, a 5T / 5T+ grid of 317 moves. It could be the best possible 5T and 5T+ final grid, and in consequence also
an upper bound for maximum score, but difficult to prove... This
is anyway the record for the 5T++ game. And this is also a counterexample to Flammenkamp's
"proof" above of 288 moves.
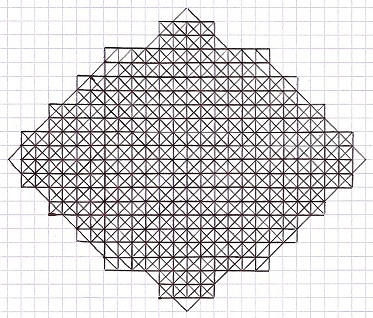
November 2011: Record
grid 5T++, best know
5T final grid, 317 moves, by Christian Boyer
i.e.
317 lines (82 horizontal + 81 vertical
+ 77 diagonal/ + 77 diagonal\) , and 317 + 36 = 353
dots
The number of initial dots has a big influence on the best possible final grid. With only six supplemental
dots (36 + 6 = 42 initial dots), we can obtain 535 moves, i.e. more than two hundred supplemental moves!
And with twelve more supplemental dots (42 + 12 = 54 initial dots), we can obtain 829 moves! I think that
these two grids are the best possible for these numbers of initial dots, but again
difficult to prove. In the three grids, the trick is the same: if you look at the four sides as stairs, each
stair has a 2x2 size, except one larger stair 4x2. With this
trick, almost all diagonal lines, but also horizontal and vertical lines,
are multiples of four segments, fully filling the inside without
leaving unused spaces.
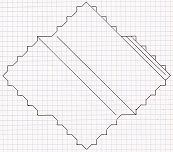
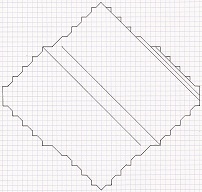
November 2011: 5T
final grid of 535 moves with 42 initial dots, i.e.
535 lines and 577 dots
and 5T
final grid of 829 moves with 54 initial dots, i.e.
829 lines and 883 dots, by Christian Boyer
Filling the grids is left
as an exercice of patience for the reader :-)
As you can see, my final grids looks
like diamonds... I mean the shape, not the gem... even if it is the trade
of Arthur Langerman ;-)
Flammenkamp used octagons only.
But maybe somebody will construct better 5T final grids,
more moves with
the same numbers of initial dots? And maybe with one more different shape?
Minimum scores
After the maximum scores, what about the minimum scores? I have
never seen any mention of them. Strange... because it is a lot of fun to construct
bad grids! Here are my worst possible grids (other examples
with the same numbers of moves are possible):
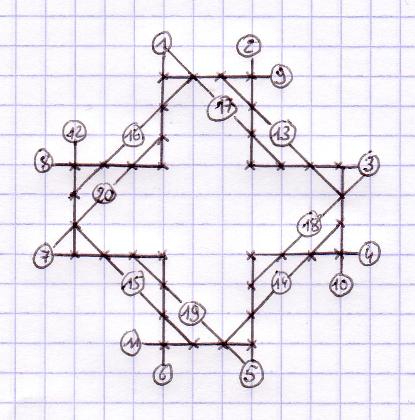
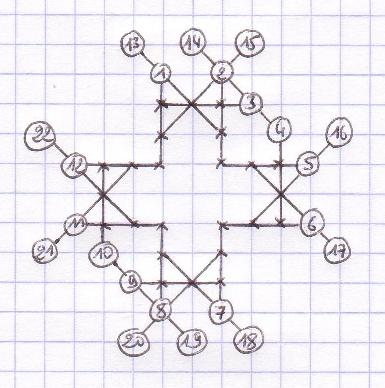
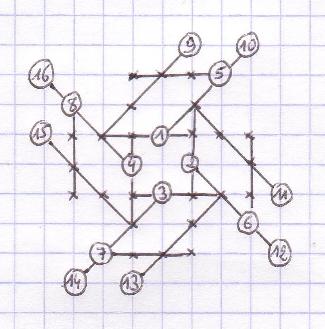
January
2008: Examples
of worst possible Morpion Solitaire games, by Christian Boyer.
Respectiveley 5T/5D game
with 20 moves, 4T game with 22 moves, 4D game with 16 moves.
(click on the
images to enlarge them)
Look at the 22 moves of the worst possible
4T game: it is strangely impossible to get a grid as bad as the 5T and 5D games
(20 moves).
During his enumeration,
Michael Quist confirmed in March 2008 that my scores are the worst possible,
and computed the number of different possible grids:
- worst 5T = 20 moves (39 distinct terminal
positions)
- worst 5D = 20 moves (51 distinct terminal
positions)
- worst 4T = 22 moves (6 distinct terminal
positions)
- worst 4D = 16 moves (12 distinct terminal
positions)
© Christian Boyer, www.morpionsolitaire.com









