Morpion Solitaire - Record Grids (5D game)
August 21st, 2010: new 5D record with a grid of 82 moves by Christopher D. Rosin, USA, only 5 days after his 5T record!!! Two more moves than the previous 5D record by Tristan Cazenave. Chris Rosin got his result after only one hour of computation, reusing the same software that produced his 5T record. A very powerful algorithm and software!
Look at his grid below or see the animated GIF file (2.1Mb, created by C. Rosin) showing the game, move by move.
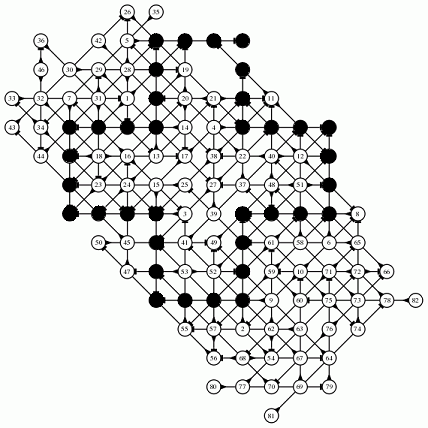
August
2010: Grid of 82 moves done by computer by
Chris Rosin (click on the image to enlarge it)
In May 2011, Chris Rosin announced that the new enhanced version of his program, able to produce a new 5T record, has unfortunately been unable to produce a new 5D record. However, good results because, after 82 runs of his app, one hour for each run, 25 of them produced grids of 82 moves, which equals 25 times his previous record!
Here are 19 grids, Chris does not have images of the 6 missing grids. After rotations/symmetries, I have oriented these images in the same direction as his first record of 2010, we can better see that they are extremely close... See the Powerpoint presentation (2.1Mb), or its equivalent PDF file (2.3Mb). Quite the same, including the same strange "hole" in the Greek cross. What I thought below on Cazenave's grid of 80 moves was wrong: finally not so rare to have a hole in a good grid...
May 2011: New grids of 82 moves by Chris Rosin, compared to the grid of 2010 (click on the images to enlarge them)
Two grids of 82 moves were found in 2012 by Tristan Cazenave using his new Monte-Carlo algorithm called "Beam search". He also reused, separately, the NRPA (Nested Rollout Policy Adaptation) algorithm of Chris Rosin inspired by his works of 2009, but improved with this beam search: he did not obtain a better score, but this improved algorithm is interesting for the traveling salesman problem with time windows, a very difficult version of the old classical salesman problem. Look at papers published from 2009 to 2012 by Chris Rosin, and by Tristan Cazenave (and Fabien Teytaud).
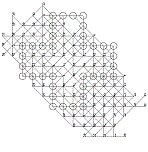
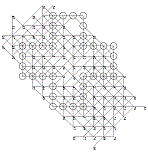
2012:
Two grids of 82 moves by Tristan
Cazenave.
For a better comparison, grids are here oriented after rotations/symmetries
in the same direction as Rosin's grids.
The first one is the same as
Rosin's 82e, and the second one is very close to
Rosin's 82d and 82i.
 Tristan Cazenave (Paris 1968 - ) in 2008
Tristan Cazenave (Paris 1968 - ) in 2008
Before 82 moves, the previous record was a grid of 80 moves by Tristan Cazenave, obtained by computer February 1st, 2008. Tristan Cazenave, a well-known specialist of the Go game, had already written papers on Morpion Solitaire and had already been the record-holder with his grids of 76 and 78 moves. He was assistant professor at the LIASD (Laboratoire d'Informatique Avancée de Saint-Denis, University of Paris 8), http://www.ai.univ-paris8.fr
November 3rd, 2008: another grid of 80 moves found by Tristan Cazenave. He is now professor at the LAMSADE (Laboratoire d'Analyse et Modélisation de Systèmes pour l'Aide à la Décision, University of Paris-Dauphine). His home page is http://www.lamsade.dauphine.fr/~cazenave
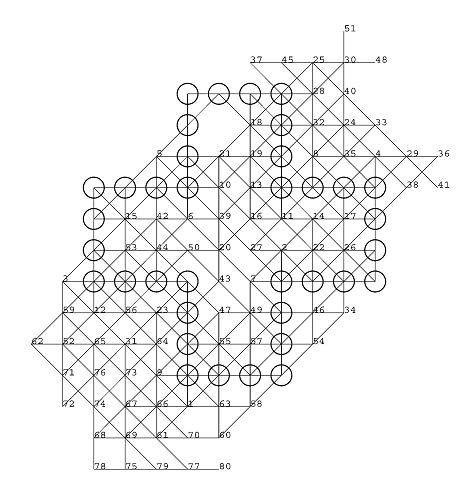
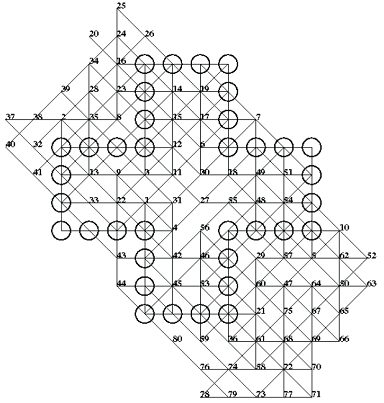
2008 (February on the left, November on the right): Grids of 80 moves done by computer by Tristan Cazenave
My own feeling is that Cazenave's records above can still be improved. Look at the 4 unused potentials of the November 2008 grid: 20-24-26, 38-32-41, 75-67-65 and 77-70-66. And look at those in the south-west corner of the February 2008 grid: alignments 71-76-73, 63-70-79 and 72-68-75. Leaving so many unused potentials in so small a zone usually offers, after slight modifications in the moves, a better solution. And it is rare to see a record grid with a hole, here on the left of move 18. But after my own tries, I am unable to improve his grid. I succeeded in using his 63-70-79 potential adding one move in the south-west corner... but only if I suppress one move on the opposite north-east corner. 80 + 1 - 1 = again 80 moves...
Zbigniew Galias, Poland, has computed at the end of February 2010 that the last 47 moves of both of Cazenave's grids are optimal.

February
2008: Another grid of 80 moves by Christian
Boyer, after some modifications of the Cazenave's grid
The previous record was set 8 months earlier also by computer by the Finnish team Heikki Hyyrö and Timo Poranen, University of Tampere. They used a simulated annealing algorithm described in their "New Heuristics for Morpion Solitaire" paper. For this kind of algorithm, look at http://en.wikipedia.org/wiki/Simulated_annealing or http://mathworld.wolfram.com/SimulatedAnnealing.html.
June 2007: Grid of 79 moves done by computer by Heikki Hyyrö and Timo Poranen
In his "Reflexive Monte-Carlo Search" paper at CGW 2007 (Computer Games Workshop), Tristan Cazenave published this grid of 78 moves.
May 2007: Grid of 78 moves done by computer by Tristan Cazenave
For the previous records of the 5D game, look at http://slef.org/jeu page by Stefan Langerman. Some old records were found by hand, without computer.
Analyzing the symmetrical grids by computer, Michael Quist, USA, found this grid of 68 moves in April 2008. He thinks that it should be the best possible score of all symmetrical 5D grids (inversion symmetry like this one, but also diagonal reflection, horizontal reflection, 90-degree rotation, ...).
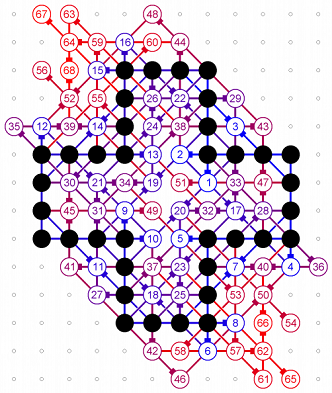
April
2008: symmetrical grid of 68
moves done by computer by Michael Quist
© Christian Boyer, www.morpionsolitaire.com